There is something magical about tin. Tin is the familiar faint silvery metal that kids used to cast into figures. You know, before computers could make much better looking figures, that are also animated and interacting.

Tin is special because it has the greatest number of stable isotopes. More precisely, there are 10 of them. So this entry is a bit unusual, it is not about one single nuclide, but more about the element tin and about magic. We have already covered the case of technetium that doesn’t have a single stable isotope, and then tin has ten of them. How can this be so, what makes tin so special?

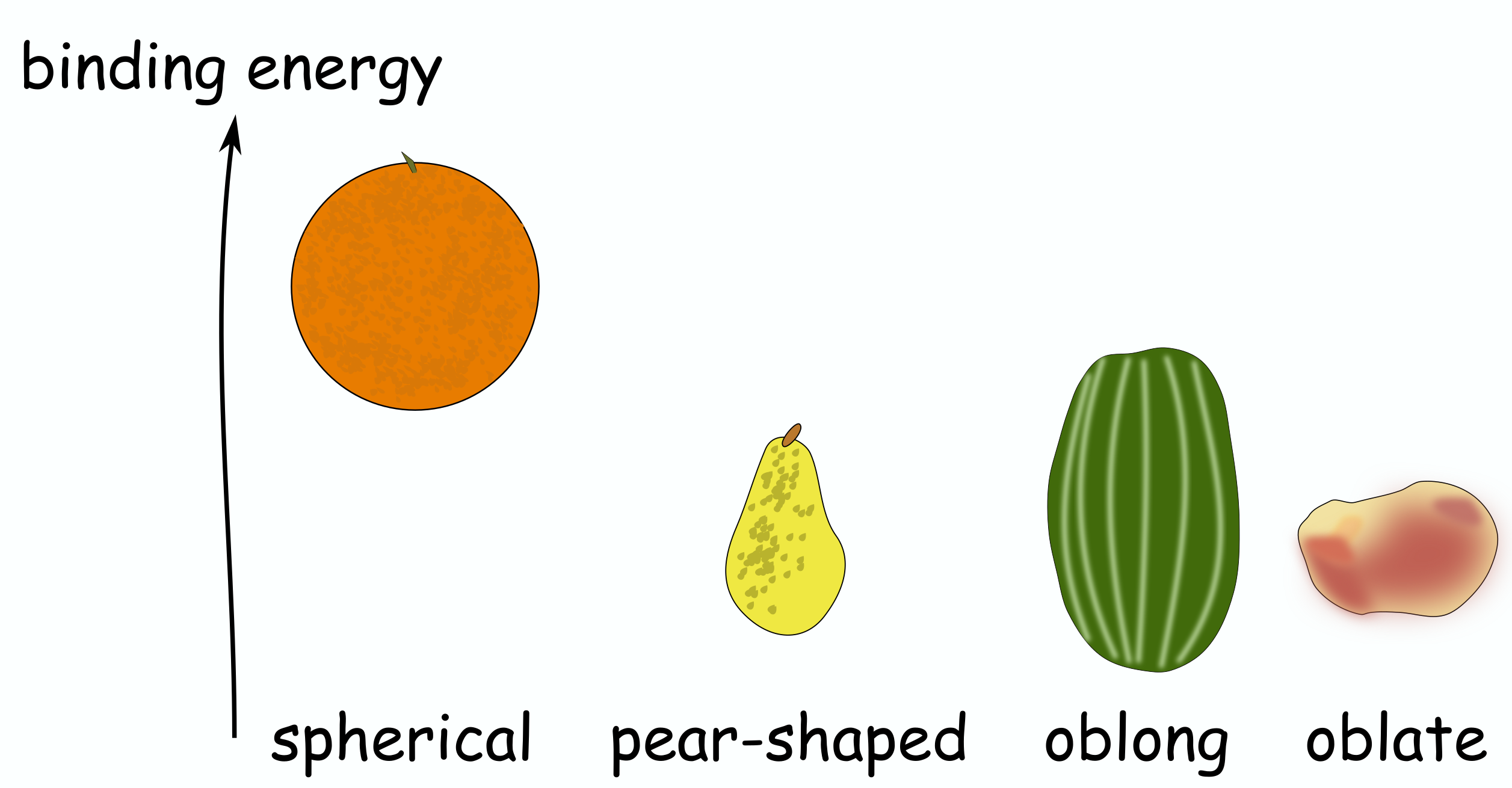
It was found in the 40-ies that if the number of protons or neutrons in the nucleus were some particular numbers, then the binding energy was higher, thus making these nuclei more stable than otherwise expected. Maria Goeppert Mayer coined the term “magic numbers” for such numbers, starting with 2, 8, 20, 28, 50, and 82. Tin isotopes happen to have 50 protons, being in that series. The existence of magic numbers was evidence that the nucleons within the nucleus organize themselves in shells, similar to electrons around the nucleus. Once a shell is filled, the binding energy per nucleon is higher than for the subsequent nuclides, because they are required to start filling nucleons on the next shell, which is less energetically favoured. This is analogous with atoms with completely filled electron shells that are very stable and do not participate in chemical reactions, those are the noble gases. Nuclei can have various shapes: oblong, oblate, even pear-shape, however full shells in nuclei typically result in lower deformation energy, and these nuclei exhibit a spherical shape.

Interestingly, there are expectations of islands of stability for nuclides that are very heavy. Such islands of stability would be doubly magic, so that both the neutrons and protons appear at magic numbers, thereby preventing the nuclides there from decaying. However, it remains difficult to synthesize such nuclides, so it is not known to what extent they’d really be stable.